1. 확률의 정의
-어떤 사건의 발생에 대해 장래 발생의 비율을 수치로 표현한 것
| 과거의 발생률 | 미래의 발생률 |
| 비율 | 확률 |
-어떤 특정 사건이 일어날 가능성을 0~1사이의 값으로 표현
-확률이 0에 가까우면 어떤 사건이 일어날 가능성이 낮고, 1에 가까우면 일어날 가능성이 높음
2. 고전적 확률과 통계적 확률
가. 고전적 확률
| 조건 | 우연실험에서 일어날 수 있는 경우가 N가지로 유한 각각의 경우가 일어날 가능성이 모두 동일 어떤 사건 A가 일어날 수 있는 경우가 M가지일 경우 |
| 사건 A가 일어날 확률 | P(A) = M/N |
| 고전적 확률의 한계 | 일어날 수 있는 경우가 모두 알려져 있고 각각의 사건이 일어날 가능성이 모두 동일한 경우에 적용 실제 문제에서는 조건을 만족하지 못하는 경우가 자주 발생 |
-과학적 실험이나 자연 현상에 대한 오랫동안의 관측을 통하여 "동일한 상황 하에서 실험이나 시행을 반복할 때 특정한 사건이 일어날 횟수는 어떤 일정한 법칙을 따른다"는 경험 관찰
나. 통계적 확률
| 조건 | 동일 상황 하에서 실험이니 시행을 n번 반복할 때 어떤 사건 A가 일어날 횟수를 fn(A)라 하면 횟수 n이 충분히 큰 경우 |
| 통계적 확률 | 사건 A의 상대도수 = fn(A)/n은 어떤 일정한 상수값에 수렴 (사건 A가 일어날 확률을 상대도수의 극한 개념으로 정의) |
| 비고 | 신생아가 남자일 수학적 확률 : 0.5 통계청 자료, 자연계에서의 암수 비율 : 49: 51 (51%) |
-수학적 확률이 실제 현상을 반영하지 못하므로 통계적 확률이 요구됨
3. 주관적 확률과 공리적 확률
가. 주관적 확률
| 상대도수의 한계 | 상대도수 극한 개념을 모든 사건에 대한 확률을 정의 불가 반복 실행이나 시행 불가능한 경우, 확률을 상대도수의 극한개념으로 나타낼 수 없음 |
| 주관적 확률의 정의 | 어떤 과정에서 한 결과를 얻을 확률은 사전지식, 정보, 경험 등을 바탕으로 개인의 주관적인 판단에 의해 결정 가능 개인의 확신과 정보에 기초를 두고 결정되는 확률 |
| 비고 | 개인에 따라 확률이 다르게 나타날 수 있으며 개인의 의사결정을 하는 중요 요소가 될 수 있음 새로운 벤처 사업을 시작했을 때 성공 확률 |
나. 공리적 확률
| 정의 | 수학적 확률, 경험적 확률, 주관적 확률에 포괄적 적용 가능한 형태로 정의한 확률 |
| 사건 A에 대한 확률 조건 | 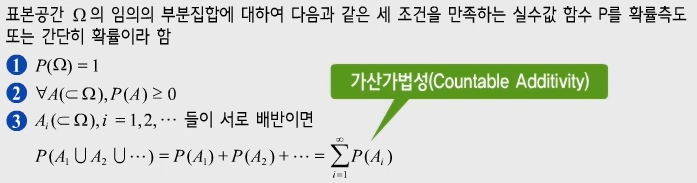 |
| 독립사건 | 독립사건, 종속사건 |
| 조건부확률 | 실험결과에 관한 어떤 일부 정보가 주어졌을 때 확률을 계산하고자 하는 경우 |



댓글