1. 가설검정
-통계분석은 우리가 알고자 하는 내용에 대해 모집단을 다 조사해야하지만 그럴 수 없어서 표본을 추출하게 되고 표본으로부터 계산된 통계량들을 근거로 모집단 판단
- 기초통계 분석방법: 독립표본 t-test, 대응 2표본 t-test, 분산분석, 상관분석, 회귀분석
- 기초통계 분석방법 적용 방법 파악과 출력 결과 해석에 어려움
- 출력된 결과 해석 방법
- 귀무가설과 대립가설
| 구분 | 기호 | 설명 |
| 귀무가설 | H0 차이가 없다 관계가 없다 |
-별다른 문제가 없는 한 나타날 것으로 예상되는 현상에 대한 기존 입장 |
| 대립가설 | H1 귀무가설에 대한 반대 입장 |
-귀무가설에 상반된 입장 -형태에 따라 '단측검정'과 '양측검정'으로 구분 |
*** 연구문제에 대한 가설 예시: 남학생들의 평균성적이 여학생보다 높다.
o 남학생들의 평균성적이 여학생보다 같거나 낮다. → 귀무가설
o 남학생들의 평균성적이 여학생보다 높다. → 대립가설
** "차이가 클수 있다"는 클 수도 있고, 작을 수 있다는 것을 의미하므로 양측검정에 해당 (양방향 모두를 주장으로 함)
o 연령대별 한달 생활비는 차이가 있다.
o 성별에 따른 선호과목이 차이가 있다.
- 가설검정 3단계
1단계 : 귀무가설과 대립가설을 수립한다.
2단계 : 검정을 위한 표본추출 또는 확률실험을 설계한다.
3단계 : 의사결정의 기준을 정한다.
2. 1종 오류와 2종 오류
- 귀무가설과 대립가설 중 어느 하나를 받아들일지 결정하는 과정 에서 범할 수 있는 오류

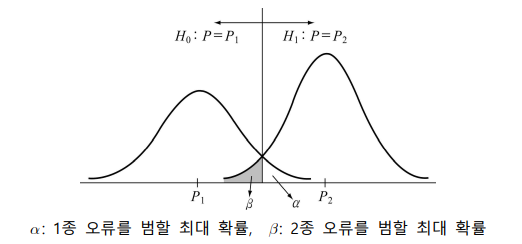
o 1종 오류(Type I error) : 귀무가설이 참일 때 귀무가설을 기각하게 되는 오류
o 2종 오류(Type II error) : 대립가설이 참일 때 대립가설을 기각하게 되는 오류
3. 유의 수준
- 의사결정 기준 수립 시 귀무가설을 받아들일지, 대립가설을 받아들일지에 대한 기준 결정
- 유의수준 사용
- 귀무가설이 참이라는 전제 하에 가설검정을 하게 되며 귀무가설이 참일 때 나타날 수 있는 결과 확인을 위해 유의수준 필요
- 유의수준 (α)은 가설검정에서 귀무가설이 실제로 참일때 귀무가설에 대한 판단의 오류 수준(1종 오류의 최대 확률)
- 실제 검정 시 유의수준을 미리 설정한 후 1종 오류를 범할 확률이 α이하가 되도록 검정 규칙을 정함
****통계교육원(통계패키지 학습을 위한 필수 통계지식) 참조
'통계학의 이해' 카테고리의 다른 글
| 표본이론 기초 (2) | 2022.08.29 |
|---|---|
| 가설검정 이해 (0) | 2022.08.26 |
| 표본추출분포의 이해 (0) | 2022.08.26 |
| 정규분포와 표준정규분포 (0) | 2022.08.26 |
| 통계 용어 정리 (0) | 2022.08.26 |




댓글