1. 정규분포
- 가우스분포
- 많은 분야에서 연속형 변수로 나타나는 현상을 표현하는 분포로 자리 잡음

- 가운데가 높고 좌우대칭적인 형태
- 중심을 나타내는 평균과 산포를 나타내는 표준편차가 형태를 결정
- 정규분포를 따른다고 가정하는 것은 평균을 중심으로 좌우대칭적인 형태의 종모양 함수를 의미

- Y축이 상대도수밀도인 히스토그램의 모습을 종모양의 함수로 표시 (면적 100%, 비율 1로 표기),
(상대도수밀도 = 상대도수/계급구간의 폭)

- 어느 지역의 1인 가구의 생활비 정규분포로 가정한 경우, 생활비는?
생활비를 평균 170만원, 표준편차 20만원일 때,
o 이 지역에 있는 1인 가구의 약 68%의 생활비는 150만원에서 190만원
(평균으로부터 1-표준편차 작거나 큰 경우)
o 190만원 이상 쓰는 1인 가구, 150만원 이하로 쓰는 가구
150~190만원 쓰는 가구는 68.26%이므로 그외의 경우가 31.74%
이를 190만원 이상, 150만원 이하 그룹으로 구분하면 15.87%가 된다.
2. 표준정규분포
- 정규분포의 특성 활용
- 평균에 따른 분포 중심 결정, 표준편차에 비례해 폭이 커짐을 활용해 하나의 정규분포확률을 통한 모든 정규분포의 확률 계산할 수 있는 표준화 기법 개발
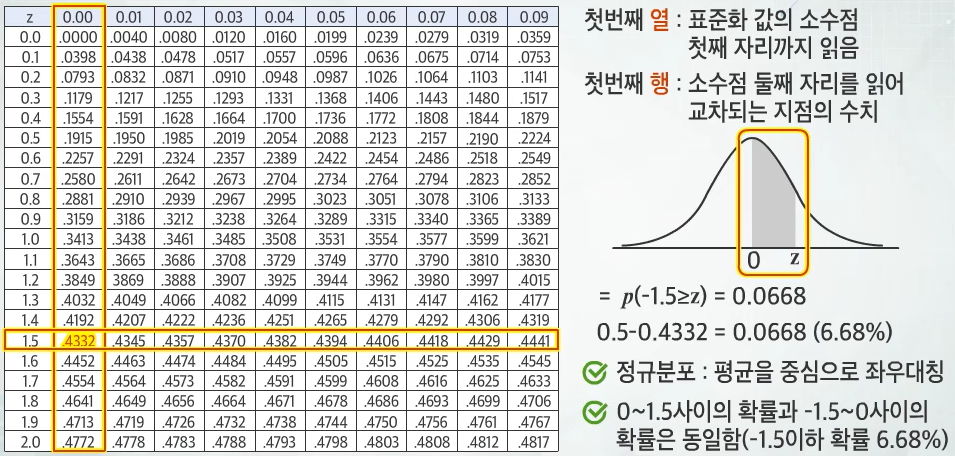
- 표준화 값 (Z) : 관찰값과 평균의 차이를 표준편차로 나눈 값 (자료의 표준화값)
- 표준화 값 (Z)는 자료값과 평균과의 차이가 그 집단의 표준편차의 몇배에 해당하는지를 알려주는 값

- X가 정규분포를 따를 때 분포의 특징

- Z의 특징

- 표준화 값(Z)을 통해 어떤 값에 해당하는 표준화 값을 통한 상대적 위치 파악 가능
****통계교육원(통계패키지 학습을 위한 필수 통계지식) 참조
'통계학의 이해' 카테고리의 다른 글
| 가설검정 (0) | 2022.08.26 |
|---|---|
| 표본추출분포의 이해 (0) | 2022.08.26 |
| 통계 용어 정리 (0) | 2022.08.26 |
| 23. 이항분포와 (표준)정규분포 (0) | 2021.08.16 |
| 22. 확률분포와 확률질량(밀도)함수 (0) | 2021.08.16 |




댓글