1. 이항실험과 이항분포
가. 이항실험(binomial experiment)
-각 시행에서 성공확률이 p인 베르누이 시행을 주어진 횟수(n번)만큼 반복할 때 각 시행이 독립적이기 때문에 각 시행의 결과가 다른 시행의 결과에 영향을 미치지 않으면 우리는 전체 실험을 이항실험이라 함
-베르누이 실험을 독립적으로 n번 반복 시행하는 것
예)
-표적에 3발을 쐈을 때 과녁에 맞히면 h라 표시하고 못 맞히면 m이라 표시
-각 시행은 독립적이며 h와 m의 확률도 동일
-h가 나올 횟수는 0, 1, 2,3 중 하나 (X가 나올 값)
-한번 쏘아서 과녁을 맞힐 확률 p

나. 이항분포(binomial distribution)
-이러한 이항실험의 성공 횟수 확률분포를 이항분포라 함
-베르누이는 이항분포의 특수한 경우임 (n=1)

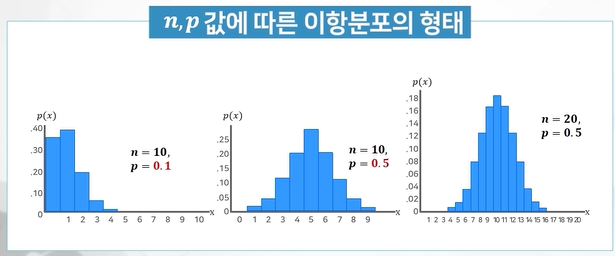
-이항분포에서 기댓값과 분산

2. 정규분포
가. 정규분포의 정의
-많은 자연, 사회현상들의 확률분포는 종모양의 곡선으로 표현 가능하며 이러한 곡선을 정규 곡선이라 하며 확률분포를 정규분포라 함
-(관련된 사회 현상) 키, 몸무게, 수명, 성적, IQ, 투자수익율, 매출액, 경제성장률, 불량률 등
-평균을 중심으로 골고루 분포된 현상
-연속형 확률변수의 분포를 정규분포라 가장하면, 확률변수가 취할 수 있는 값의 모든 범위에서 확률 계산 가능
-표본으로부터 모수 추정을 위한 통계량의 정확도 파악 가능
나. 정규분포의 성질
-평균과 표준편차를 통해 표현
-표준편차 양수 값만을 가짐




3. 표준정규분포
가. 표준정규분포의 정의
-평균이 0이고 분산이 1인 정규분포를 표준정규분포라 함
-확률변수를 Z로 나타내며 다음과 같이 정의

나. 확률변수 X의 중심화와 단위화

-표준화는 확률변수에 중심화와 단위화를 같이 시행하는 것
X가 정규분포를 따를 때 확률변수 Z는 표준정규분포를 따름 -> 확률변수 Z가 표준정규분포를 따른다고 할 때 Z가 일정 구간 [a, b] 내의 수치를 취할 확률은 표준정규분포표나 통계 프로그램을 이용해 쉽게 구할 수 있음
다. 표준정규분포표

예)

-표준정규곡선은 z=0에 대하여 대칭이므로 z가 0보다 큰 부분의 면적을 알고 있으면 z가 0보다 작은 부분은 산출 가능
P(Z >= a) = 1 - P(Z < a)
P(a <= Z <= b) = P(Z <= b) - P(Z < a)
라. 표준정규분포에서 상방백분위수 Zα의 정의
-표준정규분포에서 100(1-α) 백분위수 Zα : P(Z >= z) = α인 z값, 즉 표준정규분포의 꼬리 확률이 α가 되게 하는 z값

마. 정규확률변수의 표준정규확률변수로 변환
-정규분포에서 확률 계산은 평균과 분산을 이용하여 표준화한 표준정규곡선 아래 면적으로 대치하여 계산 가능
-정규분포 N(μ, σ^2)에서 표준화를 이용하여 P(a <= X <= b)


'통계학의 이해' 카테고리의 다른 글
| 정규분포와 표준정규분포 (0) | 2022.08.26 |
|---|---|
| 통계 용어 정리 (0) | 2022.08.26 |
| 22. 확률분포와 확률질량(밀도)함수 (0) | 2021.08.16 |
| 21. 확률의 성질 (0) | 2021.07.31 |
| 20. 공분산과 상관계수 (0) | 2021.07.30 |




댓글