1. 공분산
가. 공분산의 정의
| 분산, 표준편차 | -평균을 중심으로 흩어지거나 밀집되는 정도를 나타내는 척도 |
| 공분산 | -두개의 확률변수의 선형관계를 나타내는 값 -독립변수와 종속변수(x, y)가 흩어지거나 밀집되는 방향과 정도를 나타내는 척도 (한 확률변수의 증감에 따른 다른 확률변수의 증감 경향에 대한 척도) |
-분산이라는 개념을 확장하여 두 개의 확률변수의 흩어진 정도를 나타냄
나. 공분산의 유형
| 모공분산 | -독립변수의 편차와 종속변수의 편차의 곱에 대한 평균 |
| 표본공분산 | -독립변수의 편차와 종속변수의 편차의 곱의 합을 n-1로 나눈 값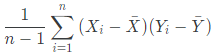 |
다. 공분산과 산점도
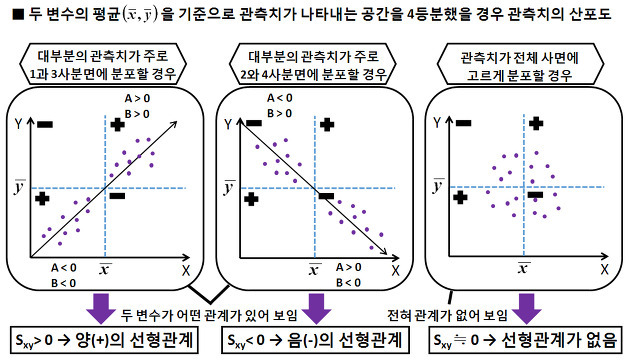
-'Sxy > 0'이면 '양의 상관관계', 'Sxy < 0'이면 '음의 상관관계', 'Sxy = 0'이면 '무상관관계'가 있다고 함
-공분산이 양수이고 절대값 클수록 두 자료 x와 y는 강한 양의 상관관계
-공분산이 음수이고 절대값이 클수록 두 자료 x와 y는 강한 음의 상관관계
2. 상관계수
가. 상관계수의 정의
-두 변수가 분포되어 있는 밀도를 표현하는 척도
-공분산을 표준화한 척도
-공분산을 각각의 Sx(x의 편차)와 Sy(y의 편차)의 곱으로 나눈 값

나. 상관계수의 유형
| 구분 | 설명 |
| 모상관계수 | -두 모집단 x와 y에 대한 모표준편차를 각각 σx, σy라 하고 모공분산 σxy라 할 때 |
| 표본상관계수 | -두 표본 x와 y에 대한 표본표준편차를 각각 sx, sy라 하고 모공분산 sxy라 할 때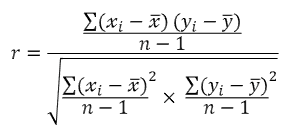 |
| 일반화 상관계수 공식 | 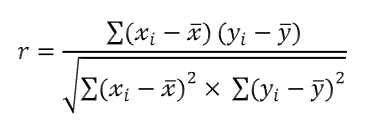 |
다. 상관계수의 특성
| 상관계수 관계 | 설명 |
| rxy = 1 | x와 y는 완전 양의 상관관계 |
| rxy > 0 | x와 y는 양의 상관관계를 갖고 양의 기울기를 갖는 적합선이 존재 |
| rxy = 0 | x와 y는 무상관관계 또는 비선형관계가 존재 가능 |
| rxy < 0 | x와 y는 음의 상관관계를 갖고 음의 기울기를 갖는 적합선이 존재 |
| rxy = -1 | x와 y는 완전 음의 상관관계 |

*상관분석
-두 변수가 서로 어떤 관계에 있는지를 파악하는 분석 (양/음 상관관계)
'통계학의 이해' 카테고리의 다른 글
| 22. 확률분포와 확률질량(밀도)함수 (0) | 2021.08.16 |
|---|---|
| 21. 확률의 성질 (0) | 2021.07.31 |
| 19. 상자그림 (0) | 2021.07.29 |
| 18. 백분위수와 사분위수 (0) | 2021.07.29 |
| 17. z-점수 (0) | 2021.07.29 |




댓글