1. 표본조사의 개요
가. 표본조사의 정의
-모집단을 잘 대표할 수 있는 조사단위의 일부만을 조사하는 것
-전수조사가 불가능하거나 전수조사가 가능하지만 비용, 시간 등의 면에서 표본조사가 선호되는 경우에 사용
-전수조사란 모집단(통계 집단)을 구성하는 조사단위를 전부 조사하는 것
나. 표본조사의 장점
- (경제성), 조사비용이 전수조사에 비해 적게 듦
-(신속성), 신속한 정보를 적시에 얻을 수 있음
-(정확성), 표본조사를 하게 되면 표본오차가 발생하나 전수조사보다 비표본오차가 작게 발생
-(심도 있는 조사), 인구주택총조사는 20개 항목은 전수 조사하고 나머지 50개 항목(전수조사항목 20개, 추가 항목 30개)은 표본조사로 심도 있는 조사 가능
-(파괴검사), 자동차 안전도 검사나 전구 수명 등 측정 시 표본조사만 가능
-표본조사가 합리적, 과학적으로 이뤄지면 전수조사보다 오차를 줄여 정확한 조사 결과를 얻을 수 있음
2. 표본조사에서 쓰이는 개념(용어 정의)
| 구분 | 설명 |
| 기본단위 | -조사의 대상이 되는 가장 최소의 단위 (예) -가계소비조사 : 가구 |
| 모집단 | -조사대상이 되는 기본다위들의 집합 -표본조사를 실시하고자 할 때 우선 모집단을 명확히 규정 (유한모집단/무한모집단) (예) 서울시 가구당 월평균소득 조사 -기본단위 : 서울시 각 가구 -모집단 : 서울시 모든 가구 o 목표모집단 -통계조사에서 관심 대상이 되는 모든 기본단위들의 집합 o 조사모집단 -현실적으로 조사가 가능하고 추출틀을 작성할 수 있는 추출단위들로 구성된 모집단 o 추출틀의 정확성 -목표모집단 Ut와 조사모집단 Us간의 차이로부터 측정 가능 -Ut = Us이면 추출틀은 목표모집단에 대해 완전하다고 함 -불완전 추출틀: 기본단위의 과소포함, 과대포함, 중복된 목록 1) 과소 포함 추출틀: -목표모집단의 기본단위 > 조사모집단 (목표모집단의 일부가 조사모집단에 존재하지 않는 경우) 2) 과대 포함 추출틀: -목표모집단의 기본단위 < 조사모집단 (목표모집단에 존재하지 않는 단위가 조사모집단에 존재) 3) 중복된 목록 -목표모집단의 기본단위가 추출틀에 한번 이상 나타날 때 |
| 추출단위 | -모집단에서 표본을 추출하기 위해 설정한 기본단위들의 집합 -기본단위와 추출단위가 서로 상이할 수 있음 -추출단위를 기본단위와 동일하게 할 것인지에 따라 추출틀 작성이 달라질 수 있음 o 추출단위와 기본단위가 같은 경우 -여론조사에서 개인을 표본으로 선택할 경우, 기본단위와 추출단위가 모두 개인으로 동일 o 추출단위와 기본단위가 다른 경우 -여론조사에서 가구를 표본으로 선택할 경우, 기본단위는 개인, 추출단위는 가구 *추출단위의 조건 -기본단위는 모두 어느 한 추출단위에 포함 -기본단위는 두개이상의 추출단위에 동시 포함 불가 -추눌단위는 조사현장에서 확인 가능, 추출작업이 용이 |
| 추출틀 or 추출대장 | -표본추출단위들로 구성된 목록 -표본조사에서 표본은 실제적으로 추출틀로부터 뽑히기 때문에 추출틀 작성이 필수, 추출단위를 결정할 때부터 미리 추출틀을 작성할 수 있는 추출단위들로 고려 *추출틀의 요건 -정의된 모집단 내의 모든 추출단위들을 포함 -어느 추출단위도 중복 불가 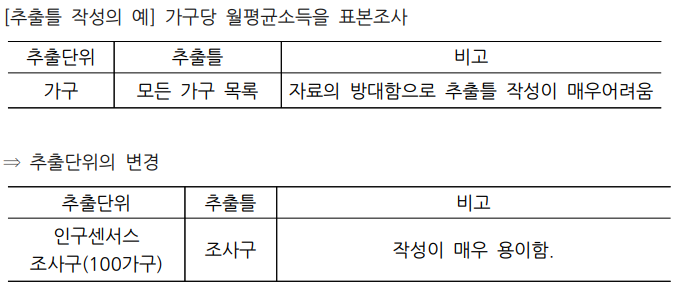 *추출틀의 종류 -명부틀: 가구나 개인을 추출단위로 하여 목록이나 명부 작성 가능한 경우 -지역추출틀: 시, 면과 같이 일정한 지역을 추출단위로 정의하는 경우  |
| 표본 | -추출틀로부터 뽑은 추출단위의 집합 |
| 표본추출 | -확률추출법 모집단을 구성하고 있는 모든 추출단위가 표본으로 추출될 확률을 사전에 알고 있는 표본추출법 -비확률추출법 각 추출단위들이 표본으로 추출될 확률을 객관적으로 나타낼 수 없는 추출법 |
| 표본오차 | -모수와 표본추정치의 차이 -모집단으로부터 선정된 표본이 어느 정도가지 정확하게 모집단의 특성을 반영하는가를 측정  -표본오차를 구하기 위해서는 세타값을 알아야 하지만 이는 모수로써 실제는 알 수 없음 (표본오차 계산 불가, 표본통계량의 표본분포의 성질을 이용하여 평균적인 표본오차를 구함) |
| 평균제곱오차(MSE) | -Mean Square Error -모수와 추정량의 편차의 제곱의 기대값 -표본조사에서 추정량의 정확도를 측정하는데 사용 -비편향추정량의 정확도(accuracy)라 함 -MSE와 분산과의 관계  |
| 표준오차 | -비편향추정량의 표준오차(standard error) -분산의 양의 제곱근인 |
| 정도 | -비편향추정량의 정도(pression) -신뢰계수를 z로 표시하면 추정치와 모수의 관계를 다음과 같이 표현 가능 |
| 추정 | -표본조사에서 추정량의 요구사항은 비편향성과 유효성임 |
| 변동계수 | -CV(Coefficient of Variation) -추정량의 표준오차가 추정량의 형태에 따라 달라짐으로 이를 해결하기 위한 방법으로 변동계수를 이용함  |
****통계교육원(통계패키지 학습을 위한 필수 통계지식) 참조








댓글