1. 통계적 추론의 개요
가. 통계적 추론
-표본으로부터 얻은 정보를 이용하여 모집단에 관한 추측이나 결론을 이끌어내는 과정
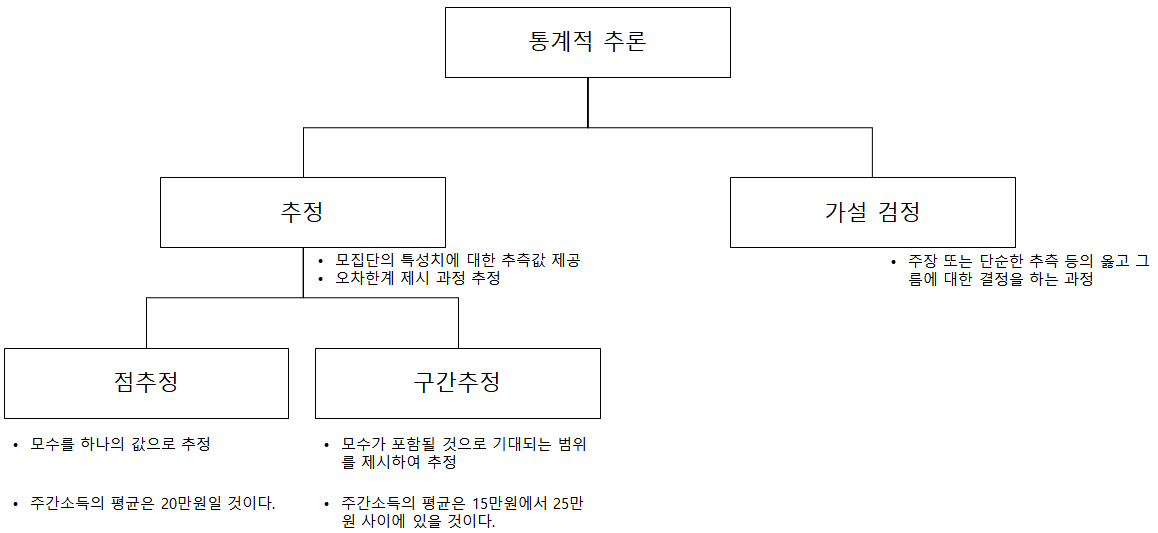
나. 통계적 추론의 종류
2. 점추정
가. 점추정의 정의
-(추정) 모집단의 특성치에 대한 추측값을 제공하고 그 오차한계를 제시하는 과정
-(점추정) 모수를 하나의 값으로 추정하는 과정
-점추정은 불확실한 정도를 표현하지 못하는 단점을 가지고 있어 구간추정과 같이 고려해야 함
나. 점추정 관련 용어
| 구분 | 설명 | 예시 |
| 모수 | 관심의 대상인 모집단의 특성 | 모평균, 모비율 |
| 추정량 | 모수를 추정하기 위해 사용되는 통계량 | 표본평균, 표본비율 |
| 추정치 | 어느 특정한 표본으로부터 구한 추정량의 계산된 값 | 계산된 표본평균값 |
| 추정 | 모집단의 특성인 모수를 추정하는 일련의 과정 |
-표준편차인 표준오차는 신뢰도를 나타내는 아주 중요한 측도이다. 따라서 표준오차의 제시 없는 추정치는 무의미한 결과이며 최소한 표본의 크기는 주어져야 함
다. 점추정에서 대표 모수 추정량
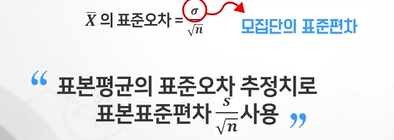
-표본평균의 표준오차는 모집단의 표준편차를 이용해 구할 수 있으나 이 값은 알 수 없는 경우가 많아 표본평균의 표준오차 추정치를 이용

라. 좋은 점추정량 성질

-추정량이 다르면 표본이 같다고 하더라도 다른 추정값이 나오므로 어느 추정량을 사용할 것인지 선택 필요
| 구분 | 설명 | 특징 |
| 불편성 (불편 추정량) | -추정량의 평균이 모수와 일치하는 추정량 -기대값 : 다른 표본 선택 시 추정량의 값이 변하므로 무수히 많은 표본으로부터 얻어진 추정치의 값들의 평균 |
 |
| 효율성 | -추정량의 분산이 작은 것 -추정량의 분산이 작으면 추정량이 변하는 정도가 작다는 의미 -특정한 표본에서 계산된 추정치 값이 더 신뢰성이 높다는 의미 |
 |
| 일치성 (일치 추정량) | -표본의 크기 n이 증가할수록 추정량 θ(엣)이 모수 θ에 더욱 근접하는 추정량 |
-불편추정량 중에서 분산이 가장 작은 추정량을 최소분산불편추정량이라 함
3. 구간추정
가. 구간추정의 정의
-관심이 있는 모수 θ가 포함될 것이라고 기대하는 구간을 추정하는 방법
나. 구간추정의 특징
(정확성) 가장 정확한 통계를 얻기 위해서는 모집단에 대한 통계 이용 필요
(오차) 모집단이 아닌 표본을 이용하여 추정할 경우 항상 오차 발생
(표현) 신뢰수준과 표준오차를 이용하여 추정값의 정확도 표현
다. 구간추정 관련 용어
| 구분 | 설명 | 특징 |
| 신뢰구간 | -모수가 포함될 것이라고 기대하는 구간 |  |
| 신뢰도 | -추정값의 불확실한 정도 표현 -신뢰구간에서 신뢰수준 95% 각각의 표본으로부터 얻은 신뢰구간 중 95%에 해당하는 구간이 모수 θ를 포함, 나머지는 모수 θ를 포함하지 않는다는 의미 |
 |
라. 모평균 μ의 신뢰구간을 구하는 방법
1) 모집단이 정규분포를 따를 때 (모분산 σ^2을 알 때)

-모평균의 추정량인 표본평균의 분포가 정규분포인 것을 이용
-정규분포 분위수와 표준오차를 이용
-모집단의 표준편차 σ를 모를때는 사용할 수 없으며 모분산은 알지만 모평균을 모르는 경우는 현실적으로 많지 않음
-현실적으로는 모분산과 모평균을 모르는 경우가 대부분임
2) 모집단이 정규분포를 따를 때 (모분산 σ^2을 모를 때)
-σ의 추정량인 표본분산 S를 대입
-표준오차 대신에 표준오차의 추정량을 사용
-이때 통계량은 표준정규분포를 따르지 않고 자유도가 n-1인 t분포를 따름

3) 모집단이 정규분포를 따르지 않을 때
-모집단의 분포가 정규분포라는 가정이 없는 경우 중심극한정리를 이용하면 표본평균의 분포가 근사적으로 정규분포를 따른다는 사실을 이용하여 근사 신뢰구간을 구할 수 있음
-모평균의 신뢰구간
모집단의 분포가 정규분포가 아닌 임의의 분포이더라도 n이 충분히 큰 경우 표본평균은 근사적으로 정규분포를 따름

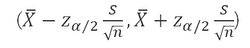
마. t-분포


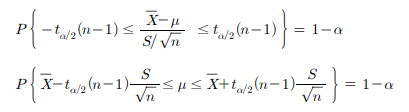

-t분포의 모양은 표준정규분포와 유사한 종모양이며 0을 중심으로 대칭 구조
-평균과 멀리 떨어진 꼬리 근처에 밀도가 표준정규분포보다 높음 (t분포에서 평균과 멀리 떨어진 자료들이 더 많다는 의미)
-자유도 (n-1) 즉 표본의 크기가 커지면 정규분포와 매우 유사한 모양
'통계학의 이해' 카테고리의 다른 글
| 14. 통계적 가설검정 (0) | 2021.07.18 |
|---|---|
| 13. 모평균 및 모비율의 신뢰구간 구하기 (0) | 2021.07.18 |
| 11. 표본분포 (0) | 2021.07.17 |
| 10. 베르누이 실험과 분포 (0) | 2021.07.17 |
| 09. 확률변수 (0) | 2021.07.13 |




댓글