1. 표본분포(Sampling Distribution)
가. 표본분포의 정의
-표본의 특성을 나타내는 통계량의 확률분포
-모집단에서 크기 n인 표본을 반복하여 선정할 때 얻어지는 통계량의 확률분포
-표본평균, 표본분산과 같이 표본으로부터 계산 가능한 확률변수의 분포
-모집단의 모든 자료값을 알고 있는 경우는 드물기 때문에 표본을 선정하여 모집단의 특성을 추론 (추론 통계학)
나. 용어 정의
- (통계량) 표본평균, 표본분산과 같이 표본의 특성을 나타내는 표본으로부터 계산 가능한 확률변수
- (표본평균, 표본분산)

- (모비율, 표본비율)
모비율, p = x / N
표본비율, p(바) = x / n
(예시)
어느 연구자가 어느 대학교의 학생의 주당 TV 시청 평균 시간에 관심이 있다고 한다. 이를 위해 연구자는 임의로 100명의 학생들을 추출하여 각 학생들의 주당 TV 시청시간을 조사한 결과, 100명의 학생 TV 시청시간 의 평균이 25시간이 나왔다. 이를 근거로 연구자는 이 대학교 학생의 주당 TV시청 평균시간은 25시간이라 고 추정하는 결론을 내릴 것이다. 이 결론이 타당한 것인가?
(모집단) 연구 대상인 이 대학교의 전체 학생
(관심 있는 연구 대상의 전체 집단 또는 연구 대상의 특성에 대한 모든 값의 집합)
임의로 선택한 학생들의 TV 시청시간을 확률변수 X로 정의하면 분포가 실제 평균(μ)을 중심으로 골고루 펴져 있음
(모수) 연구자의 관심사로 모집단의 특성인 주당 TV 평균시간
(모집단의 특성을 나타내는 수)
모평균(μ), 모분산(σ^2), 모표준편차(σ)
(표본) 모집단인 일부인 추출된 100명의 학생
(집단의 일부를 표본이라 하며 동일한 모집단에서 독립적으로 뽑힌 표본을 랜덤표본 혹은 확률표본, 임의표본이라 함)
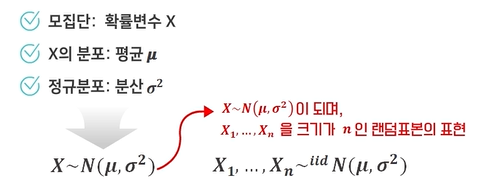
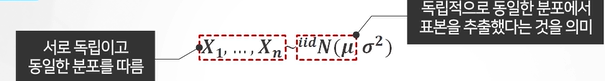
(통계량) 표본으로부터 계산되는 값으로 100명 학생의 주당 TV 시청에 대한 표본평균
(표본으로부터 계산 가능한 표본의 특성값)
랜덤표본 X1, X2, .... Xn의 함수이며 확률변수의 함수이므로 확률변수가 됨
(검정통계량) 검정을 하기 위해 사용하는 통계량

-표본이 달라지면 표본평균이 달라짐
-표본평균의 분포를 알아야 연구자가 계산한 25시간이라는 결과의 근거 제시 가능
2. 표본평균의 표본분포
가. 모분산을 아는 경우
-모집단이 정규분포를 따르면 표본평균들도 정규분포의 선형결합이므로 정규분포를 따름
-따라서 평균과 분산을 쉽게 계산 가능
-(표준오차) 표본평균의 표준편차이며 다른 랜덤표본을 뽑았을 때 평균적으로 값이 흔들리는 정도
표준오차가 작다는 것은 다른 랜덤표본을 뽑았을 때 값이 적게 변하는 것으로 추정량 값이 신뢰가 있다는 것을 의미
-정규 모집단 N에서 크기 n인 표본을 복원추출할 경우

표본평균 X(바)의 평균과 분산은 다음과 같음


나. 모분산을 모르는 경우
-모분산(σ^2)이 알려지지 않은 정규분포 모집단에서 크기 n인 표본을 추출할 때 표본평균 X(바)의 표분화 확률변수를 T로 나타냄
-표본평균 X(바)의 표준화에서 모표준편차 σ를 표준편차 s로 대치하면 X(바)의 표준화 확률변수는 자유도가 n-1인 t-분포가 됨

-또한 표본 크기 n이 클수록 표본분산 s^2은 모분산 σ^2에 근사하므로 n이 충분히 크면 모평균 μ이고 모분산은 알려지지 않은 모든 모집단에 대해 중심극한정리가 성립함


다. 모집단이 정규분포를 따르지 않는 경우
-모집단이 정규분포를 따르지 않을 경우 모분산을 알 때와 모를 때 중심극한정리 또는 t-분포에 따라 X(바)의 표본분포를 구할 수 있음

3. 기타 표본분포
가. 표본비율의 표본분포
-표본을 구성하는 개개인이 특정 사건에 대해 선호하는 비율이 독립적으로 p이므로 표본으로 선정된 n명 중 특정사건을 선호하는 사람의 수를 X라 하면 X~B(n, p)임
-표본비율 p(바)의 평균과 분산은 다음과 같음
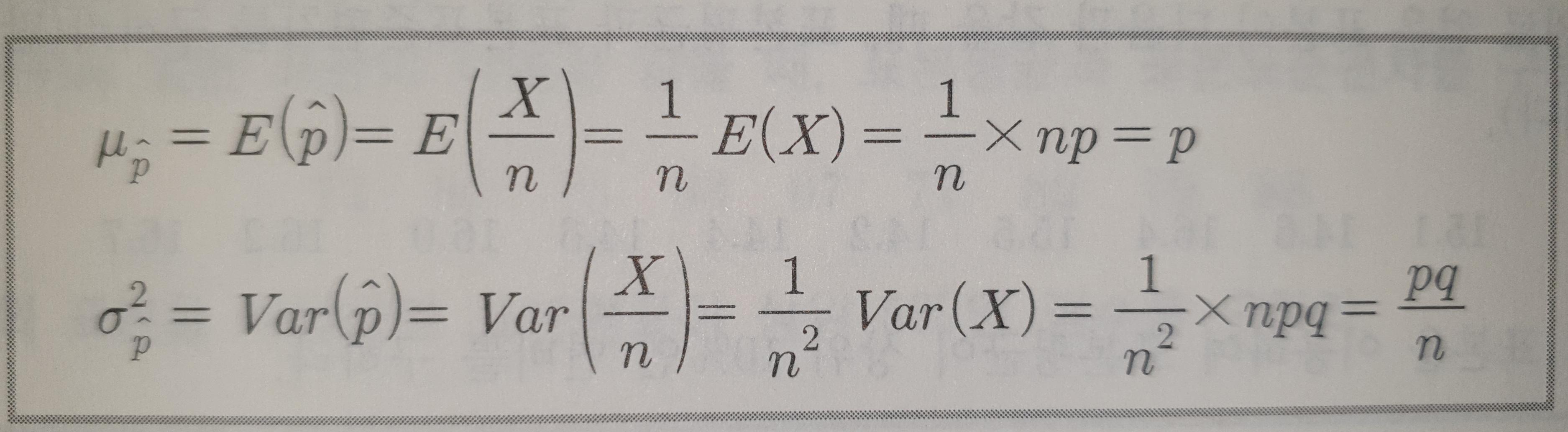
4. 중심극한정리
-n이 커질수록 X(바)의 분포는 정규분포에 근사함

'통계학의 이해' 카테고리의 다른 글
| 14. 통계적 가설검정 (0) | 2021.07.18 |
|---|---|
| 13. 모평균 및 모비율의 신뢰구간 구하기 (0) | 2021.07.18 |
| 10. 베르누이 실험과 분포 (0) | 2021.07.17 |
| 09. 확률변수 (0) | 2021.07.13 |
| 08. 조건부 확률 (0) | 2021.07.13 |




댓글