1. 조건부 확률의 개요.
가. 조건부 확률의 정의
-P(A|B)
-사상 B가 주어진 조건 하에서 사상 A가 발생할 확률 (사건 B 중에서 사건 A의 비율)
-'|'는 given에 해당하는 기호
나. 조건부 확률의 특징
| 구분 | 관련 공식 | 설명 |
| 곱셈 법칙 |  |
-조건부 확률 공식의 양변에 P(B)를 곱하여 곱셈 법칙 유도 가능 |
| 독립 사상 | 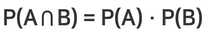 |
-다른 사건의 발생 확률에 영향을 주지 않는 경우 -두 사상 A와 B가 독립이라는 것은 사상 B가 일어났다는 조건 아래 사상 A가 일어날 조건부 확률이 사상 A가 일어날 확율과 같다. -주사위 두번 던지기 |
| 종속 사상 | -다른 사건의 발생 확률에 영향을 주는 경우 -위 독립사상 등식이 성립하지 않는 경우 종속사상 -비가 오는지 여부와 우산가게 매출 |
다. 독립사건과 배반사건 관계
| 배반사건 | P(A∩B) = 0 이지만 P(A) ∙ P(B) ≠ 0 임 P(A∩B) ≠ P(A) ∙ P(B) 이므로 A와 B가 독립사건이 아님 |
| 독립사건 | P(A∩B) = P(A) ∙ P(B) ≠ 0 이므로 P(A∩B) ≠ 0 이 되어 A와 B는 배반이 아님 |
-두 사건 A와 B가 공사건이 아닌 경우에
2. 조건부 확률의 개념도 및 관계
가. 조건부 확률의 개념도 (공식)

나. P(A|B)와 P(A) 관계

3. 확률의 기본 법칙
가. 두 사건의 관계
| 구분 | 예시 | 설명 |
| 독립이다. | 소나기가 내리는 사건 삼각김밥이 팔리는 사건 |
두 사건이 아무런 관계가 없을 때 |
| 독립이 아니다. | 소나기가 내리는 사건 편의점에서 우산이 팔리는 사건 |
두 사건이 관계가 있을 때 |
나. 확률의 기본 법칙
| 구분 | 관계식 | 설명 |
| A와 B의 합사상 | 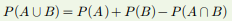 |
-A 또는 B가 일어날 사상 |
| A와 B의 곱사상 | 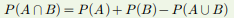 |
-A와 B가 모두 일어날 사상 |
| A와 B의 배반사상 |  |
-두 사상 A와 B가 공통원소가 없는 사상 -P(A∩B) = 0 |
| A의 여사상 | 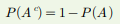 |
-A가 일어나지 않을 사상 Ac -A와 Ac는 배반적 |
다. 전확률 공식과 베이즈 정리
| 전확률 공식 | -임의의 표본 공간 S에 대하여 아래 그림과 같이 표본 공간을 서로 배반인 사건 여러 개(A1, A2,...., An)로 나눌 수 있을 때, 사건 B(P(B))를 구하는 공식(또는 방법)  |
| 베이즈 정리 | -(사전 확률) P(A1), P(A2)....P(An) -(사후 확률) P(A1|B), P(A2|B).....P(An|B) -P(B|A1)과 P(A1|B)의 차이   |
'통계학의 이해' 카테고리의 다른 글
| 10. 베르누이 실험과 분포 (0) | 2021.07.17 |
|---|---|
| 09. 확률변수 (0) | 2021.07.13 |
| 07. 곱셈법칙과 순열, 조합 (0) | 2021.07.13 |
| 06. 확률의 개요 (0) | 2021.07.13 |
| 05. 산포의 척도 (0) | 2021.07.13 |




댓글