1. 산포도의 개요
가. 산포도의 정의
- 개개의 관측값이 중심위치로부터 얼마만큼 떨어져 있는가를 나타내 주는 측도
나. 산포도의 필요성


- (동일 대푯값) 두 집단의 평균점수, 중위수, 최빈수를 각각 구해 보았더니 똑같이 60점
- (자료 퍼짐 정도) 자료의 퍼짐 정도는 다르기 때문에, 분포의 특성을 좀 더 명확하게 표현해주기 위해서는 대푯값뿐만 아니라 자료의 퍼짐성 고려 필요
- (중심 기준) 자료의 산포도는 개개의 관측값이 중심위치로부터 얼마만큼 흩어져 있는가에 따라 좌우되며 그 값이 클 수 록 변동이 크고 광범위하게 퍼져 있다는 의미
- (대표 산포도) 범위, 사분위 범위, 분산과 표준편차, 변동 계수 등
2. 산포도의 유형
| 구분 | 개념도 | 설명 |
| 범위 |  |
-주어진 데이터 분포에서 최대값 - 최소값 -범위값이 크면 데이터들이 넓게 퍼져 있음을 의미 -계산이 쉽고, 특이점에 영향을 크게 받음 |
| 평균 편차 |  |
-자료값(x)과 평균(x바)의 합은 0 -부호에 상관없이 모두 더한 값의 평균 |
| 사분위수 |  |
-데이터 값들의 50%에 포함되는 산포도 -Q3- Q1 |
| 분산 |  |
-확률변수가 기댓값으로부터 얼마나 떨어진 곳에 분포하는지 측정한 값 -편차 = xi - x평균(x바) -분산 = 편차 제곱의 평균 |
| 모 분산 | 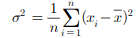 |
-x1~xn이 모집단 전체의 자료일 때 모집단 전체의 분산을 모분산 |
| 표본 분산 |  |
-x1~xn이 모집단의 일부인 n개 표본 자료일 떄 표본의 분산을 표본분산 -모집단의 퍼짐 정보를 나타내는 모분산의 추정량 |
| 표준 편차 | 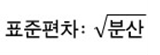 |
-표준편차 = 분산의 양의 제곱근 -모표준편차, 표본표준편차 |
| 변동 계수 |  |
-평균이 크게 다른 두개 이상의 집단이 있을 때 각 집단의 상대적 동질성을 감안한 산포도 측도 |
3. 경험적 규칙

- 일상에서 얻을 수 있는 자료의 대부분이 위의 그림과 같이 평균을 중심으로 좌우 대칭적이고, 종모양에 근접
- (68-95-99.7), 표준편차(σ, s)의 위치와 자료의 밀집 정도
- 이러한 특성은 표본 뿐만 아니라 모집단에서도 성립
3. 체비쇼프 정리 개요
-확률분포에서 데이터 샘플 또는 확률 분포가 거의 모든 값이 평균에 근접한다는 규칙
- 값 들 중 평균값으로부터 2 표준편차 이상 떨어진 것들은 1/4 이상을 차지하지 않는다.
- 3 표준편차 이상 떨어진 것들은 1/9 이상 차지하지 않는다.
- 5 표준편차 이상 떨어진 것들은 1/25 이상 차지하지 않는다.
'통계학의 이해' 카테고리의 다른 글
| 07. 곱셈법칙과 순열, 조합 (0) | 2021.07.13 |
|---|---|
| 06. 확률의 개요 (0) | 2021.07.13 |
| 04. 중심위치의 척도 (0) | 2021.07.13 |
| 03. 자료의 종류 및 시각화 (표, 그래프) (0) | 2021.07.13 |
| 02. 표본조사 (0) | 2021.07.12 |




댓글