1. 확률의 개요
가. 확률의 정의
-일정한 조건 아래에서 어떤 사건이나 사상이 일어날 가능성의 정도 또는 수치
나. 확률의 특징
-(불확실성) 알려진 불확실성을 다룰 수 있음
-(특정 사건) 모든 경우의 수에 대한 특정 사건이 발생할 비율
-(0~1) 1을 넘을 수 없고 음이 될 수도 없음
2. 확률 관련 용어 및 유형
가. 확률 관련 용어
| 구분 | 특징 | 설명 |
| 실험 | -제어 실험 -자연 실험 -현장 실험 |
-가설이나 이론이 실제로 맞는지를 확인하기 위해 다양한 조건 아래에서 측정하는 기법 |
| 통계적 실험 | -기온 기록 -동전 던지기 |
-통계적 목적 아래서 관찰이나 측정을 얻어내는 일련의 과정 |
| 시행 | -실험을 반복하는 행위 | |
| 확률 실험 | -동전 던지기 -주사위 던지기 |
-실험을 해보기 전에는 어떤 결과가 발생할지 불확실한 경우의 실험 -확률을 계산하기 위해 실험 결과를 이용하여 사건의 발생할 가능성을 측정하는 과정 |
| 표본공간 | -S로 표시 -주사위 던지기 S = {1, 2, 3, 4, 5, 6} |
-주어진 어떤 실험에서 모든 가능한 결과들의 집합 -S로 표시 |
| 표본점 | -통계적 실험을 시행할 때 나타날 수 있는 개개의 실험 결과 -표본공간을 이루는 개개의 원소 |
|
| 사상 또는 사건 | -단순사상 : 하나의 가능한 결과만 있는 사상) -임의사상 : 단순사상의 합집합 |
-표본공간의 부분집합 -표본점들만의 집합 |
| 근원사건 단순사건 |
-단 하나의 표본점으로 구성된 사건 | |
| 복합사건 | -두개 이상의 표본점으로 구성된 사건 | |
| 공사건 | -표본점이 하나도 들어있지 않은 사건 | |
| 복원추출 | -표본공간에서 표본점을 선택했을 때 동일한 표본점이 한 번 이상 반복하여 선택되도록 허용하는 추출방법 (반대의 경우 비복원추출) |
-표본공간 S의 부분집합인 A, B에 대해 합사건, 곱사건, 차사건, 여사건 정의 가능
-두 사건 A와 B가 동일한 표본점을 갖지 않는 경우 두 사건을 서로 배반이라 함
나. 확률의 유형

| 구분 | 특징 | 설명 |
| 고전적 확률 | -단순사상이 일어날 확률이 같은 등확률의 경우는 현실에 많지 않음 -표본공간의 원소 개수가 무한할 경우 고전적 정의 사용 불가 |
-사상 A가 일어날 확률을 기호 P(A)라고 할 때 -표본공간안에서 개개 표본점이 나타날 가능성이 거의 동등한 경우 |
| 경험적 확률 | -상대도수가 실험의 반복 시행 각각에 대해 동일한 극한값으로 수렴할 수 있는지에 대한 의문 증명 불가 | -실험을 직접 여러 번 반복해서 실행한 후 그중에 사건이 발생하는 횟수를 관측하여 비율로 정한 확률  |
| 공리적 확률 (기하학적 확률() |
-고전적 정의와 경험적 정의 포함 | -일반적인 경우, 표본공간 S가 주어졌을 때 어떤 사건 E가 일어날 확률 P(E) |
| 주관적 확률 | -확률에 기초한 경험이나 정보가 거의 없는 경우 | -어떤 사건이 나타날 가능성을 결정짓는 사람의 개인적인 직관이나 경험에서 우러난 추측이나 추정에 의해 정해진 확률 |
-(대수법칙) 경험적 확률은 실험을 반복할수록 고전적 확률에 가까워진다는 원칙
3. 확률의 공리적 정의

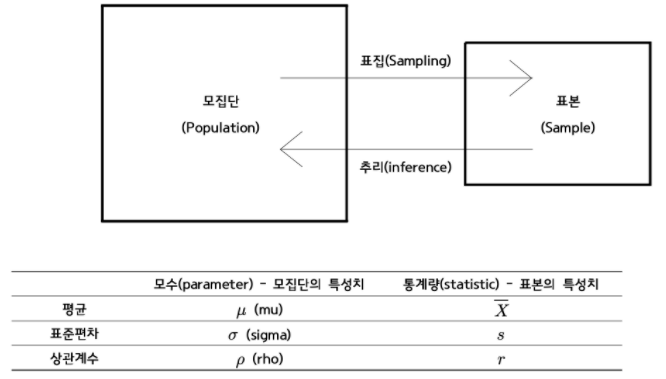
* 기타 (모집단과 표본의 특성치)
'통계학의 이해' 카테고리의 다른 글
| 08. 조건부 확률 (0) | 2021.07.13 |
|---|---|
| 07. 곱셈법칙과 순열, 조합 (0) | 2021.07.13 |
| 05. 산포의 척도 (0) | 2021.07.13 |
| 04. 중심위치의 척도 (0) | 2021.07.13 |
| 03. 자료의 종류 및 시각화 (표, 그래프) (0) | 2021.07.13 |




댓글